Apprenti Carreleur

3e primaire à 2e secondaire

Solides et figures

2 périodes de 50’ ou 1h30

Sur site & en école

À travers cette animation ludique et concrète, les élèves mettent la main à la pâte pour réaliser ensemble un pavage mural original qui pourra décorer les murs de l’école. En manipulant, ils développent leur précision gestuelle, apprennent à collaborer efficacement, à faire preuve de créativité tout en respectant des consignes techniques précises.

L’objectif ? Fabriquer des tuiles identiques en explorant activement les transformations géométriques du plan : translation, rotation, symétrie centrale et symétrie orthogonale. Une façon ludique de donner du sens aux notions abstraites de la géométrie en les vivant avec le corps… et les mains !

Observer des régularités sur un pavage.
Reconnaître et manipuler les transformations du plan : rotation et symétrie centrale (pivoter), translation (glisser) et symétrie orthogonale (retourner).
Observer un pavage tiré d’une œuvre d’art et mettre en évidence ses principales caractéristiques formelles et techniques : retrouver des formes géométriques et comprendre leur agencement sur une façade, un tableau, un tapis.
Comprendre les régularités d’un pavage, c’est-à-dire être capable de décrire et de transcrire l’enchaînement des transformations appliquées au motif qui se répète.

RÉFÉRENTIEL DE FORMATION MANUELLE, TECHNIQUE, TECHNOLOGIQUE ET NUMÉRIQUE "TRONC COMMUN"

Champ 1 : Des objets de l’espace à la géométrie

Bloc 1 : (Se) Repérer et communiquer des positionnements ou des déplacements
Savoir	Les visions de l’espace	Utiliser le vocabulaire exprimant des positions absolues : à côté de, contre, à l’intérieur, à l’extérieur, entre, sous, sur, dans, hors, autour de, face à face, dos à dos. Utiliser le vocabulaire exprimant des positions relatives (liées au regard) : devant, derrière, à droite, à gauche, en haut, en bas, au-dessus, en dessous, en face de, de face, de dos, de profil.
Savoir	Les déplacements	Utiliser le vocabulaire décrivant un déplacement : monter, descendre, avancer, reculer, s’éloigner, se rapprocher, faire demi-tour…
Savoir-faire	Situer, placer un objet ou soi-même	Exprimer la position absolue, relative ou ordinale d’un objet ou de soi-même à l’aide du vocabulaire adéquat : dans l’espace 2D (photo, plan) ; selon le point de vue de l’élève ou d’un(e) autre personnage/personne. Placer un ensemble d’objets ou soi-même selon des consignes données ou un modèle observé dans l’espace 2D.
Savoir-faire	Déplacer un objet ou soi-même	Expliquer, oralement ou par écrit, un déplacement à l’aide du vocabulaire adéquat, en identifiant des points de repère. Tracer un déplacement sur un plan, en suivant un enchaînement de consignes orales ou écrites.
Bloc 3 : Dégager des régularités et des propriétés géométriques pour construire, calculer et justifier
Savoir	Mouvements et isométries	Utiliser les termes « glisser », « retourner », « pivoter » pour décrire un mouvement appliqué à une figure. Identifier les mouvements appliqués à une figure (glisser, retourner, pivoter). Associer ces actions aux isométries correspondantes. Identifier une symétrie orthogonale, une symétrie centrale, une translation, une rotation. Reconnaître les invariants des isométries.
Savoir-faire	Réaliser des mouvements sur des figures	Exécuter un mouvement (glissement, pivotement, retournement) pour passer d’un motif à son image, à l’aide d’un support (gabarit, papier calque…). Désigner, parmi plusieurs images d’un motif, celle qui résulte d’un mouvement donné.

http://www.enseignement.be/public/docs/r-f-rentiel-de-formation-manuelle-technique-technologique-et-num-rique-fmttn-.pdf

Savoir-faire	Dégager et respecter des régularités liées aux mouvements	Réaliser une production artistique par la répétition d’un motif figuratif ou d’une figure, en appliquant des glissements, des pivotements et des retournements. Justifier que deux figures sont isométriques en identifiant l’isométrie en jeu. Justifier que deux figures ne sont pas images l’une de l’autre par une isométrie, en utilisant un argument adéquat basé sur les isométries et leurs invariants.
Domaines transversaux
Se connaître soi-même et s’ouvrir aux autres
Prendre conscience de l’espace		Situer, placer un objet ou soi-même dans l’espace 2D. Se déplacer ou déplacer un objet dans l’espace. Réaliser, dans un espace connu, un agencement spatial d’objets.

Apprendre à apprendre
Raisonner, conceptualiser, abstraire, modéliser.	Réaliser des mouvements sur des figures.
Représenter, schématiser.	Tracer/Construire des figures. Matérialiser un axe de symétrie par pliage.
Prendre conscience des apprentissages : pertinence, raisons des choix, communication.	Utiliser des propriétés pour justifier.
Développer une pensée critique et complexe
Trouver, traiter et évaluer des sources d’informations et organiser ces informations	Recueillir des informations. Choisir un paramètre ou un support adéquat pour répondre à la question posée. Critiquer des informations portant sur une même situation.
Développer la créativité et l’esprit d’entreprendre
Découvrir différentes techniques et stratégies pour résoudre des tâches	Articuler des propriétés géométriques et des procédés de construction. Construire des figures avec du matériel varié.
Découvrir le monde scolaire, la diversité des filières et des options qui s’ouvrent après le tronc commun et mieux connaître le monde des activités professionnelles
Relier des savoirs, savoir-faire ou compétences disciplinaires ou transversaux, travaillés en classe, avec des filières et des options qui s’ouvrent après le tronc commun et avec des sphères professionnelles et des métiers	Tracer des figures est une occasion de découvrir des métiers comme le graphisme, les arts…

Cette activité de manipulation permet aux élèves de réaliser collectivement un pavage qui pourra orner les murs de l’école. La précision du geste, la collaboration, la créativité et le suivi de consignes sont les ingrédients nécessaires à la fabrication de tuiles identiques !

Par groupe, les participants commencent par l’observation d’une série de pavages. Ils en dégagent les caractéristiques constitutives du pavage mathématique.

Chacun décalque ensuite une tuile d’un des pavages observés. En déplaçant ce papier calque sur le pavage, l’élève observe les différents déplacements du motif initial. La mise en commun permet de dégager les trois déplacements : glissement, pivotement, retournement.

Chaque participant suit un programme de construction pour créer sa propre tuile du poisson à partir d’une enveloppe. C’est en assemblant ces tuiles que le groupe manipule à nouveau les concepts de rotation, de translation, symétries centrale et orthogonale.

Un pavage est un recouvrement du plan par des pavés (ou tuiles), sans trou ni chevauchement.

L’observation de multitudes de pavages avec les élèves peut nous conduire à différents classements :

1. Pavages réguliers :

Les pavages réguliers sont constitués d’un seul type de polygone régulier. Il est intéressant de chercher avec les enfants combien de pavages réguliers existent. Cela permet d’aborder la notion d’angle. En effet, la somme des angles en chaque sommet est de 360°.

Pour cette raison, il n’existe que 3 pavages réguliers !

2. Pavages non réguliers :

https://www.cosmic-core.org/free/article-63-number-the-hexad-part-3-tessellations-tilings/

3. Pavages périodiques :

Ensembles de pavés pavant le plan à l’infini en se reproduisant par translations.

Ces pavages peuvent être réalisés à l’aide de polygones réguliers ou non, mais également avec des motifs qui sont des déformations de polygones….

https://images.math.cnrs.fr/un-aller-retour-au-pays-des-pavages/

4. Pavages apériodiques :

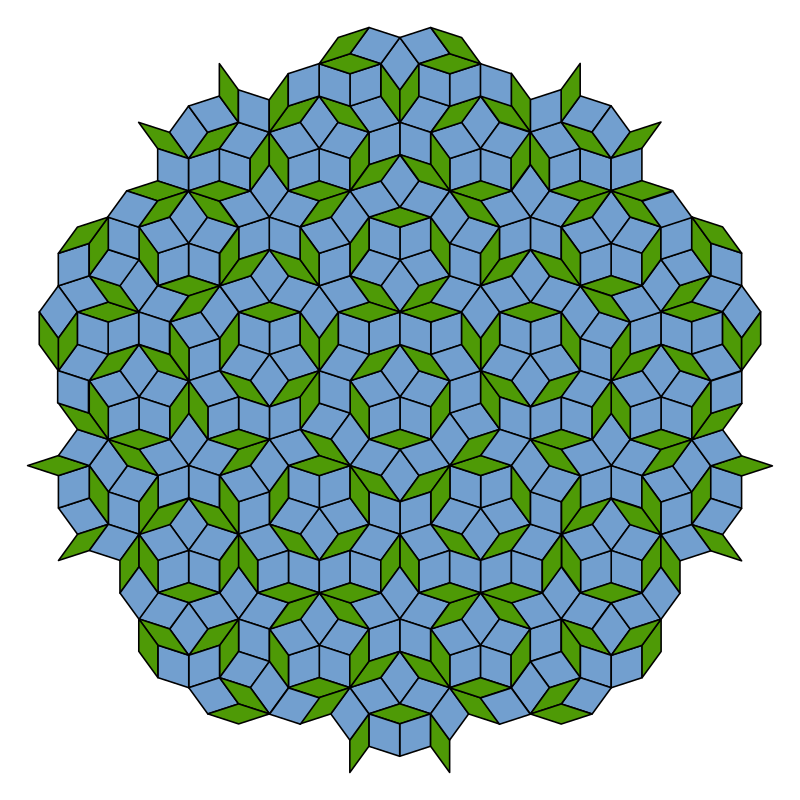
(ou non-périodiques) :

ensemble de pavés pavant le plan à l’infini, mais sans translations.

Voici un exemple : le célèbre pavage de Penrose.

https://fr.wikipedia.org/wiki/Pavage_de_Penrose

Un des intérêts pédagogiques de l’introduction de l’observation et de la construction de pavages périodiques dans les apprentissages liés aux solides et au figures réside dans la possibilité d’introduire les notions de transformations du plan. En effet, la construction d’un pavage du plan peut faire intervenir trois types d’isométries : les translations, rotations et symétries (orthogonales et centrales).

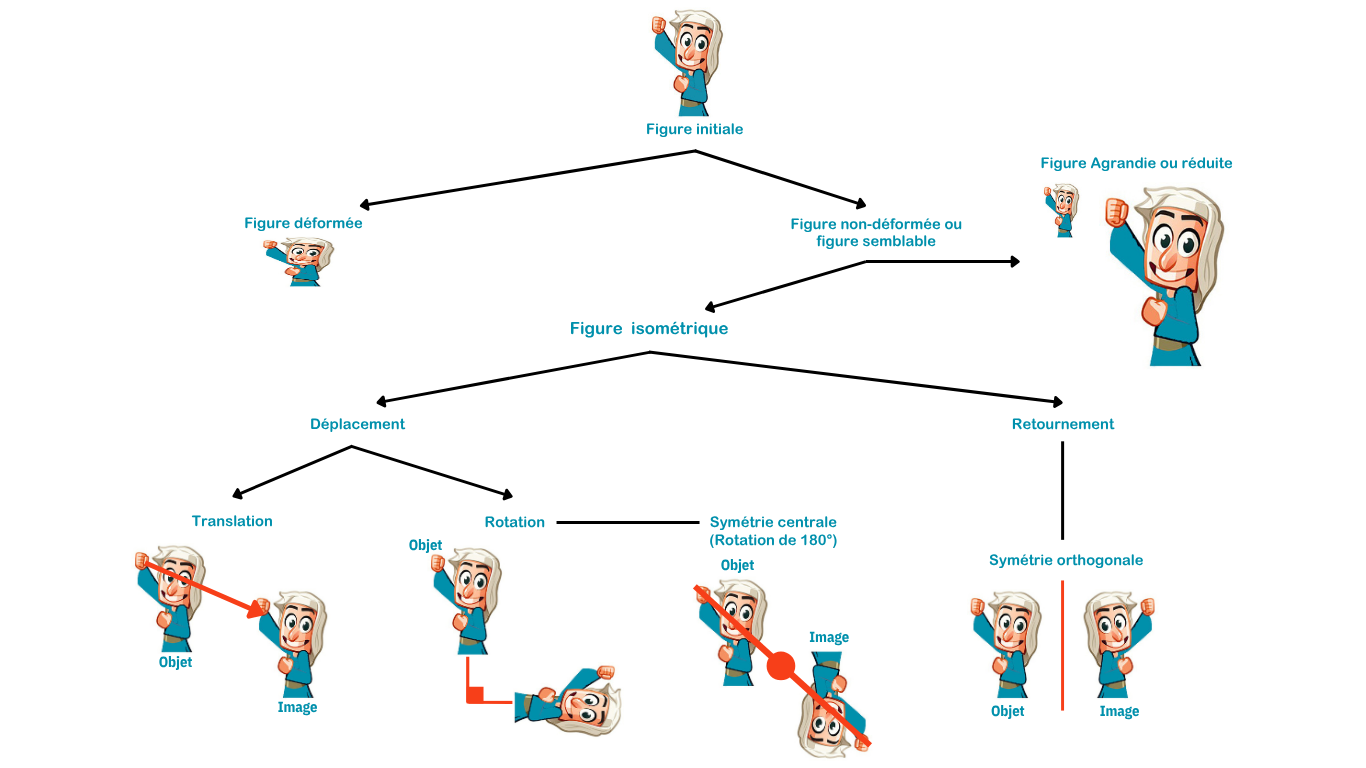
Nous pouvons dégager les caractéristiques fondamentales pour chacune de ces trois transformations :

Rotation : centre de rotation, sens de rotation (horloger ou anti-horloger), angle de rotation (180° pour une symétrie centrale)

Translation : direction (horizontalement, verticalement, en oblique), sens (vers le bas, vers la droite…), longueur ou norme du vecteur.

Symétrie orthogonale : axe de la symétrie.

Une synthèse sur les différentes transformations du plan peut être réalisée sous la forme d’un arbre dichotomique :

Des descriptions de l’activité ont été réalisées par des étudiants de l’UMons :

fiche interactive : https://view.genial.ly/624bfa275d98ba00182a6c33/guide-fiche-apprenti-carreleur-umons-and-kaleidi
Vidéo pour le professeur : https://youtu.be/pmV0gn9eJv8
Vidéo pour l’élève : https://youtu.be/AnOcjiYD9IQ

Pour revivre cette animation en classe, voici les pavages analysés lors de l’animation :

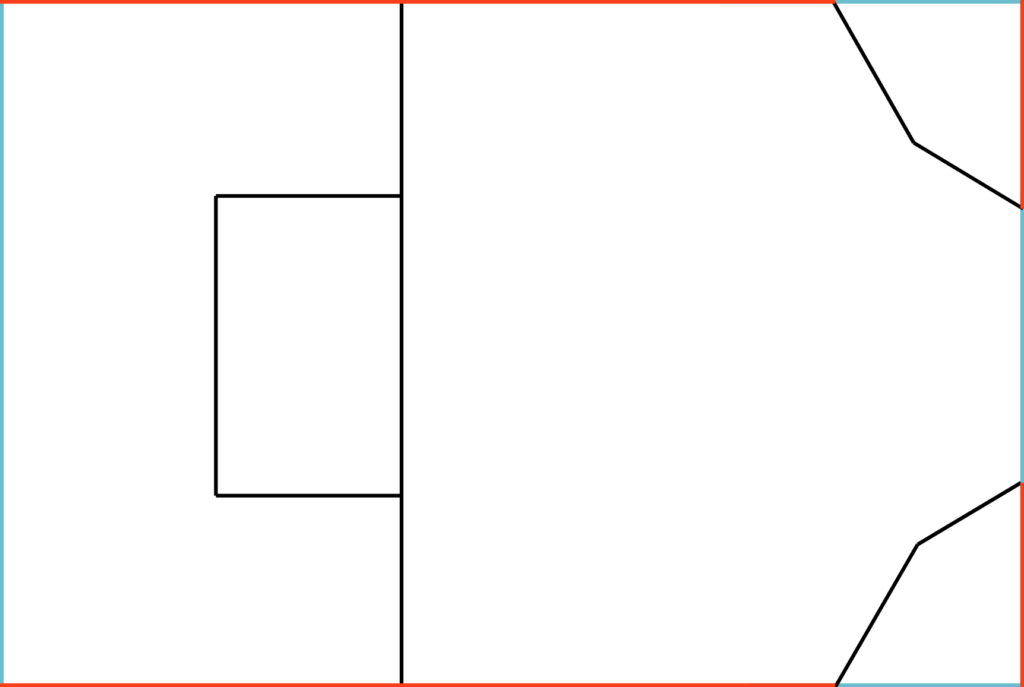
Vous pouvez ensuite reproduire la tuile « poisson », déjà rencontrée lors de l’animation, ainsi que la tuile « robot ». Il suffit, après avoir décalqué, de demander aux élèves de découper le long des lignes noires. Vous pourrez alors réaliser un deuxième magnifique pavage en classe.

Voici les deux gabarits :